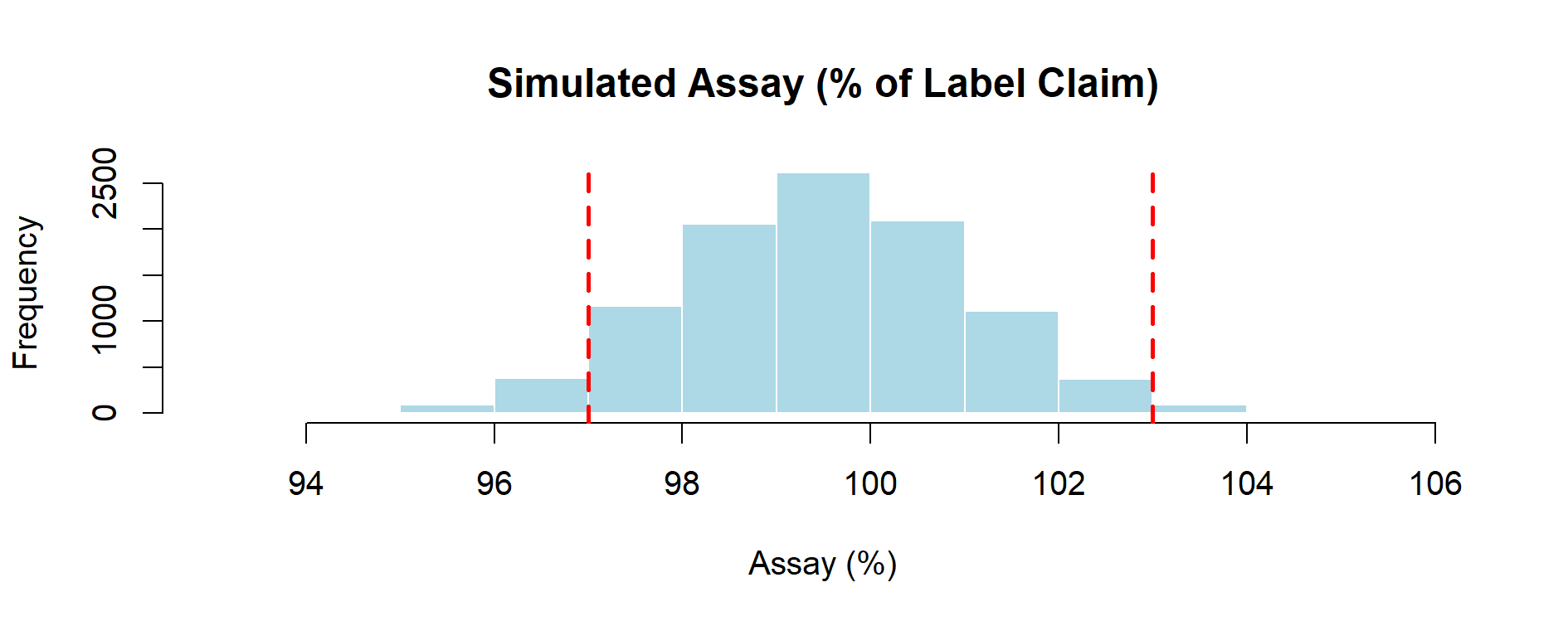
Figure 4.1 – Histogram of 10,000 simulated assay values computed via the transfer equation, with specification limits at 97–103% of label claim.
Monte Carlo simulations need a way to connect random inputs to the output we want to study.
This connection is expressed mathematically by the transfer equation.
Generic Form:
Output = f(Input₁, Input₂, ..., Inputₙ)
Suppose we want to simulate the assay of an active ingredient in a tablet:
API_weight → random variable (mg per tablet)Purity → random variable (fraction)Label_Claim → constant (mg declared on the product label)Practical note — Purity as % vs fraction In QC practice, Purity is typically reported as a percentage (e.g., 99.2%). In the transfer equation, however, it is convenient to use Purity as a fraction (e.g., 0.992) and multiply by 100 only at the end to express Assay (%). To avoid confusion, we explicitly state that Purity is handled as a fraction inside the model.
Transfer Equation:
`Assay (%) = (API_weight × Purity / Label_Claim) × 100`
⚠️ Note on terminology — Assay vs. Content
In pharmacopoeias such as USP and Ph. Eur., the result of this calculation may be reported either as assay or as content.
Both terms refer to the quantitative determination of the active ingredient, usually expressed as a percentage of the label claim.However, to avoid confusion with content uniformity (USP <905>), which is a different test assessing unit-to-unit variability,
this book consistently uses the term assay (% of label claim).
set.seed(123)
n <- 10000
Label_Claim <- 100 # mg declared on the product label
# 1. Random inputs
API_weight <- rnorm(n, mean = 100, sd = 1.5) # mg of API per tablet
Purity <- rnorm(n, mean = 0.995, sd = 0.002) # fraction purity
Purity[Purity > 1] <- 1 # clamp unrealistic >100%
Purity[Purity < 0.98] <- 0.98 # clamp unrealistic <98%
# 2. Transfer equation: % of label claim
Assay <- (API_weight * Purity / Label_Claim) * 100
# 3. Output analysis
hist(Assay,
main = "Simulated Assay (% of Label Claim)",
xlab = "Assay (%)",
col = "lightblue", border = "white")
abline(v = c(97, 103), col = "red", lwd = 2, lty = 2) # specification limits
📌 Clarification Box — Two Meanings of Transfer Equation
In simulation literature, the term transfer equation is used in two related but distinct ways:
| Context (short label) | Meaning |
|---|---|
| Technical (simulation theory – distribution generation, e.g., Hammersley & Handscomb, 1964; Ripley, 1987) | Formula that transforms a random number from U(0,1) into a random variate following a target distribution (e.g., exponential, triangular). |
| Modeling (applied Monte Carlo – uncertainty propagation, e.g., Hubbard, 2014) | The system model that combines uncertain input variables into an output of interest (e.g., Annual Savings = (MS + LS + RMS) × PL). |
👉 In this eBook, we use the modeling sense (Hubbard, 2014): the equation that transfers uncertainty from inputs (random variates) to outputs (assay, dissolution, etc.).
But remember: in the background, random numbers are first transformed into random variates using the technical definition of transfer equations.
For a more detailed discussion and examples, see the entry Transfer Equation in Chapter 11 – Glossary.
As shown in Figure 4.1, the simulated assay distribution is centered close to the target value, with natural variability leading to occasional values outside the specification limits (97–103%). This illustrates how the transfer equation connects random inputs to a realistic process output.

Figure 4.1 – Histogram of 10,000 simulated assay values computed via the transfer equation, with specification limits at 97–103% of label claim.
🔎 Note on “Label Claim” vs. “% w/w in Tablet”
In pharmaceutical QC, assay is normally expressed as a percentage of the label claim —
i.e., how much active ingredient is measured compared to the amount declared on the product label (e.g., 100 mg).
This is why specifications are usually written as 97.0–103.0% of label claim.
By contrast, the ratio (API_weight / Tablet_weight) × 100 gives the % w/w in the tablet (here ~40%).
While correct mathematically, it does not correspond to regulatory assay specifications.
For this reason, the transfer equation in this example uses label claim in the denominator.
← Previous: Simple Distributions | ▲ back to top | Next → A Complete Simulation in R